NLP: Random Forest
What Is Random Forest? Random forests or random decision forests are an ensemble learning method for classification, regression and other tasks that operate by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees. Random decision forests correct for decision trees' habit of overfitting to their training set [Wikipedia]
Classification Report: NLP Random Forest
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| Real | 0.93 | 0.92 | 0.92 | 1095 |
| Fake | 0.58 | 0.61 | 0.59 | 203 |
| Accuracy | 0.87 | 1298 | ||
| Macro Avg | 0.75 | 0.76 | 0.76 | 1298 |
| Weighted Avg | 0.87 | 0.87 | 0.87 | 1298 |
Train Time: 6.02 seconds
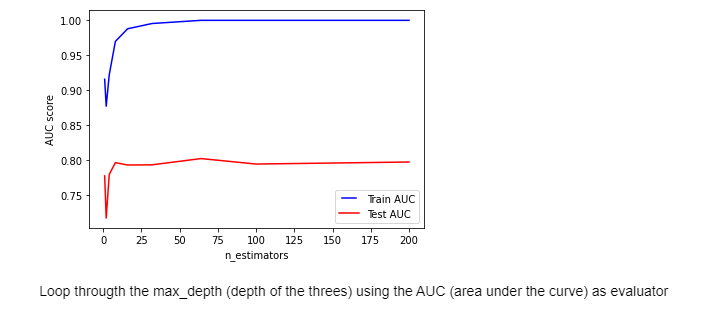
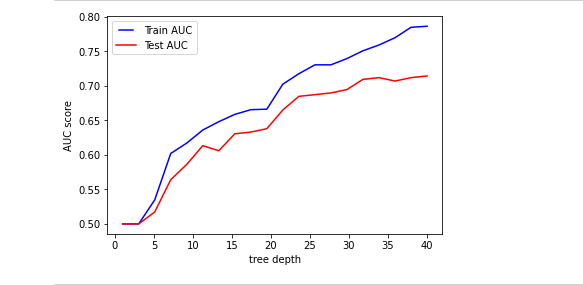
Findings: A Random Forest is a meta estimator that fits a number of decision tree classifiers on data sub-samples improves the predictive accuracy by averaging and control over-fitting. The algorithm has the advantage that it can be applied on non-normalized data. The training features can be tuned and to do that we used the AUC (Area Under Curve) as the evaluation metric. The graphs below showed the results of the parameter optimization. One aspect we took into account was that we did not need any explainability and hence we had no limitations regarding the structure of the threes/forest. The graphs are the optimization of the number of threes (n_estimator) and the depth (max_depth). The higher the number the better to learn the data. However, the addition of too many threes slows down the training process. The deeper the tree, the more splits it has and can capture more information about the data. In this case, we fitted the data of several depths and plotted the training and test errors. The python algorithm is available on the Git Repository. After the parameter optimization the model took 6.02 s to train and had a precision of .58 and .93 for the fake and real posts respectively.